Rust Image Processing DSL
This Project is essentially an attempt to recreate some of the Halide project in Rust as a means of learning that Rust language. Halide is a really clever C++ library that allows programmers to define image processing algorithms in domain specific language which are compiled according to some sort of execution strategy. These strategies might be "tile for cache efficiency" or "optimize for execution on a GPU." The project is definitely worth poking at for a few minutes.
The project I will be discussing in this blog post is an implementation of the first "half" of Halide, using Rust. Specifically, I've implemented a simple DSL for image processing which is JIT compiled with LLVM. I picked this project mostly to learn rust, so my result is certainly not production code but it may still be interesting to read a bit about.
Annotated example
Before jumping into a discussion about how all of this works, lets look at an example of the DSL. In this example, we will define the sobel operator, then process an images with it. For a great overview of the sobel operator, check out this article.
In the DSL, there are things to worry about: Functions and Chains. A function is a single unit of work that takes an \((x,y)\) coordinate and an arbitrary number of inputs. For example, suppose we have a function \(Grad(x,y)\) that returns the magnitude of the gradient of two images \(I_1\) and \(I_2\) at the point \((x,y)\). We might denote this function with mathematical notation as:
\[ Grad(x,y) = \sqrt{I_1(x,y)^2 + I_2(x,y)^2} \]
In the DSL I have defined, we would denote this operation in a similar manner, sans syntactic differences:
// create a new function named grad
// Function::new takes a number and a lambda as an argument.
// The number indicates how many inputs the function has
// This lambda is always called with (x,y) coordinate values
// and an array of inputs of the length specified.
let grad = Function::new(2, |x, y, inputs| {
// first we pull out references to the InputExpressions representing our inputs
let input0 = &inputs[0];
let input1 = &inputs[1];
// compute the squares using the input expressions
// Notice that x and y are both treated like functions.
// This is essentially a hack to get around the way I've stored the AST
let t1 = input0(x(), y()) * input0(x(), y());
let t2 = input1(x(), y()) * input1(x(), y());
// Compute the sum and the square root of the sum
// The last expression generated by this lambda is result of the function we are defining
// The Box::new trick is needed, again, because of the way I've store the AST
Box::new(SqrtExpr::new(t1 + t2))
});
This isn't the most beautiful way to build a representation of our function, but it works and I learned a lot implementing the magic that makes it work.
Each function stores is a syntax tree representing the expression that the function computes.
The syntax tree defined by the grad function looks something like this:
There is also helper function that can be used to generate functions which perform a convolution on a single image with a kernel matrix For example, to generate a function that takes a single image as input and returns the convolution with the horizontal sobel matrix, use the following code:
let sobel_x = [[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]];
let sobel_x = Function::gen_3x3_kernel(sobel_x);
Notice that these functions are defined in a purely functional, mathematical sense. They do not mutate their inputs, nor do they store any state, nor are they coupled to any particular inputs.
Connecting functions
Now that we have some abstract functions, we need to compose functions to create something meaningful. The composition of functions in my DSL is called a function chain. Chains may be thought of as a stream of pixels, starting from =ImageSource=s, flowing through a number of transformation functions, and finally, resulting in a new image. ImageSources define the starting inputs for the entire chain. Then, any number of functions may be chained together. For example, the entire sobel image processing chain looks something like this:
let sobel_x_fun = // define the sobel_x function as shown above
let sobel_y_fun = // define the sobel_y function similar to the sobel_x function given above
let grad_fun = // define the gradient function, exactly as given above
// make an ImageSource defining the start of the chain
// In this case, we only need a single image source
let image = ChainLink::ImageSource(0);
// image source pixels flow into sobel_x
let c1 = ChainLink::link(vec![&image], &sobel_x_fun);
// image source pixels flow into sobel_y
let c2 = ChainLink::link(vec![&image], &sobel_y_fun);
// pixels from sobel_x and sobel_y flow into the gradient function
let c3 = ChainLink::link(vec![&c1, &c2], &grad_fun);
Compiling and executing the chain
Now that we have built a chain representing the entire sobel algorithm, we only need to compile the chain and use the chain to process an image:
let cc = c3.compile(); // create a compiled chain for this chain
let resulting_image = cc.run_on(&[&my_image]);
Invoking .compile() on an image chain compiles each function in the chain provided into an LLVM module, optimizes the module with LLVM's optimizer, and uses LLVM's MCJIT to compile to machine code.
A compiled chain essentially just holds a function pointer to a function which will be called when the chain is executed (and some things used for bookkeeping).
The only work I had to do to go from AST to function pointer is code generation.
For this reason, LLVM is decidedly awesome.
Note: For the full sobel code, see sobel.rs.
Details, Details, Details
There's lots of little details which may be interesting to discuss, but I'm only going to discuss the compilation method. First, we need some slightly more rigorous definitions of things:
- All of the user defined functions take two 64 bit integer values and a list of inputs. They return a 64 bit integer value.
- Because functions themselves have no concept of chaining (the gradient function doesn't call
sobel_xandsobel_y), the "inputs" to a user defined function can be thought of as function-pointers which will eventually be resolved to real functions, although this is not how they are implemented. - All of the system-defined expressions (eg.
SqrtExpr) take a 64 bit integer and return a 64 bit integer.
The compilation strategy for the DSL is very simple: Every DSL function is compiled into a function with a signature that would look something like this in C:
inline int64_t function(int64_t x, int64_t y, image inputs[], size_t num_inputs);
The array of image inputs provided here is not equivalent to the list of the inputs given to the DSL function.
The inputs given to the DSL function are resolved to other compiled functions (using the chain) during code generation, so our generated grad function will directly call the sobel_x and sobel_y functions.
Since every value is a 64 bit integer, the code generation for an expression essentially just involves spitting out adds and multiplies for integers.
The generated grad code roughly corresponds to:
inline int64_t grad(int64_t x, int64_t y, image inputs[], size_t num_inputs) {
int64_t partial1 = sobel_x(x, y, inputs, num_inputs) * sobel_x(x, y, inputs, num_inputs);
int64_t partial2 = sobel_y(x, y, inputs, num_inputs) * sobel_x(x, y, inputs, num_inputs);
int64_t partial3 = partial1 + partial2;
return core_isqrt(partial3);
}
Execution and image inputs
A driver function is injected into the module. This function performs some bookkeeping tasks, then just loops over the pixels in the output image, calling the appropriate function (whichever was last in the chain) for every pixel:
for (int x = 0; x < output.width; x++) {
for (int y = 0; y < output.height; y++) {
int64_t res = function(x, y, inputs, num_inputs);
/* output image at x, y */ = (uint8_t) res;
}
Image inputs (the actual images we are processing), are passed to each function.
When the compiler reaches an ImageSource in the function chain, it emits a call to a function which returns the pixel in the image at a given \((x,y)\) coordinate.
For anyone interested, I've dumped the entire LLVM IR module for an unoptimized sobel chain here.
Some of the code is generated from the file core.c in the github repo for the project, if you need some hints to figure out what's going on here.
The entry point is the function jitfunction.
There's lots of other interesting little idiosyncrasies in this code but I don't have space and you don't have time to read about all of them.
Performance
Anyone who knows a little bit about computers and performance is probably hurting a little bit thinking about how this might perform.
You've noticed all of the function calls, don't these have lots of overhead?
Uou've noticed that I'm computing the sobel_x and sobel_y values twice in the gradient function.
Don't worry, it isn't quite so bad.
Anyone who knows a fair amount about computers and performance noticed that inline keyword and is wondering if I'm somehow relying on function inlining to extract performance from this technique.
The answer is yes.
Every generated function is marked with an LLVM attribute AlwaysInline which, when combined with the appropriate LLVM optimization passes, guarantees that these functions will always be inlined into their caller.
Aside: Function inlining
For those who are not totally familiar with the concept of function ininling, here's a quick example (note that the inline keyword in C doesn't guarantee this behavior, it is just a hint to the compiler):
// before AlwaysInlinePass
inline int foo() { return 12; }
int bar() {
for (size_t i = 0; i < 100; i++) {
if (foo() > 13) return 1;
}
return 0;
}
// after AlwaysInlinePass
int bar() {
for (size_t i = 0; i < 100; i++) {
if (12 > 13) return 1;
}
return 0;
}
It may seem that this optimization is useful because it removes function call overhead.
This is true, but it isn't the only critical reason that the optimization is useful.
Many compiler optimizations cannot (or do not) cross function boundaries.
Instead, they often view functions as black boxes about which nothing can be known (this is obviously an oversimplification).
This often makes sense because functions may be defined in different compilations units or in shared libraries, where the compiler cannot access their source.
Function inlining allows the compiler to "see" inside functions, then perform additional optimizations which would not have been possible otherwise.
For example, because the call to foo has been inlined, the compiler can now (easily) optimize the function bar to:
int bar() {
return 0;
}
Impact
Aggressive function inlining gives me lots of freedom in my code generation.
I can generate code which is totally inefficient, then inline everything and let the compiler do some of its magic.
If course, this isn't a general rule, but for this problem the generated code is highly uniform, doesn't do much with memory (other than reading from readonly images), and has a few other compiler freindly properties.
It the end of the day, LLVM is doing a pretty good job turning my functional style code into a big fat loop and eliminating redundant computations.
If you're interested in looking at the optimized sobel LLVM module, here it is: gist.
Numbers
To benchmark this code, I compared the JITed code with an implementation of the exact same thing written directly in Rust. My benchmarking is not extremely rigorous, but I've taken steps to try to create an honest benchmark.
Benchmarking environment:
- single core, 3.75GB RAM Google cloud compute virtual machine
- Ubuntu 16.04
- Rust stable (1.10.0)
- LLVM 3.9, built from source. Release build with assertions disabled
- Sobel code presented above
The benchmark input was a 1.2 gig collection of 3255 images of various sizes, ranging from 160x120 to 6922x6922 pixels. The image sizes were mixed to try to stave off cache effects and other size-related effects so that I could hopefully just use averages to compare performance.
Long story short, the average JIT/native speedup is 1.05x, so the LLVM JITed code is 1.05x faster than the direct Rust implementation (this AST construction time and compile time). This means that my JIT compiled code runs at the same speed (subject to some jitter) as the native rust code.
Here is a plot of image vs average speedup (the images are sorted by the total number of pixels in the image):
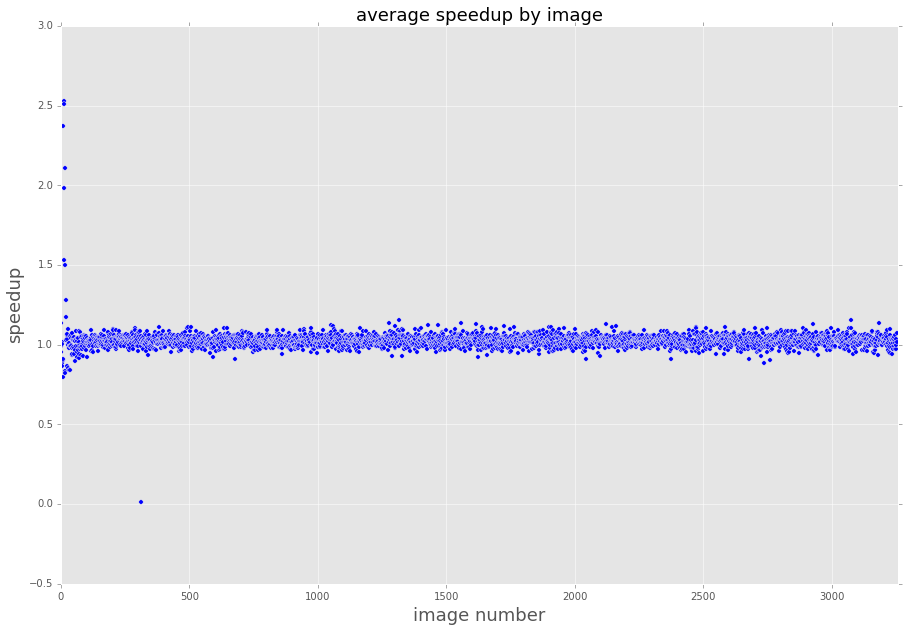
There are many more plots, but the overall conclusion is pretty clear: compared to the Rust, I'm not performing very poorly. Is this a win? I am not sure, I would need to do many more comparisons. These results do indicate to me that I have at least achieved reasonable performance, with a dramatically different programming style.
Final performance notes
It should be noted that these results are not entirely surprising. Rust is also using LLVM as a backend. It is probably reasonable to assume that the code Rust is generating looks pretty similar to the code I am generating, although I have not verified this.
If you've been nodding your head along with me, I have a confession to make: I've tricked you a little bit. LLVM is doing an awesome job (considering the code I've generated), but I'm certainly missing out on lots of opportunities for performance because of my code generation technique. Also, LLVM (or any compiler) should never be expected to be able to totally understand the problem a piece of code is trying to solve and optimize it perfectly. To really get good performance, I would need to pay attention to caching and quite a few other things which I have totally ignored. Hand tuned code should (and certainly would) run in circles around the code JIT compiled algorithm I've generated here.
If you want something that gives you an awesome DSL AND all sorts of control over cache scheduling and whatnot, take a look at Halide. If you have no idea what I'm talking about or why any of this matters, take a look at Halide anyway. The Halide talks give fantastic descriptions of many of the problems it aims to solve.
Conclusions
Overall, this project was extremely enjoyable. I had yet another opportunity to fiddle with LLVM, which is always lots of fun (but sometimes very painful). I learned a little bit about image processing and some of the challenges that arise when shuffling pixels around. Finally, I learned a little bit of Rust. I have only one thing to say about Rust: Rust is an amazing language. Go learn Rust.