Study Groups Pt. 1
Almost without fail, whenever my friends and I get together to study for something in a group, we end up in a group that, due to it's size, decreases our productivity. I'm reading a book at the moment about animal behavior, and one of the chapters referenced some research done about animal group formation. In some models, with simulation, it can be shown that groups almost always grow to be larger than their optimal size. In this post I will discuss a preliminary attempt at modeling the behavior of study group formation using similar methods. In later posts I plan to strengthen the model and (hopefully) present possible solutions to the problem.
The Model
The basic assumptions of the simulation we will use are as follows:
- When a person "arrives" they must chose a study group to join (can't walk away)
- People arrive one at a time
- Once someone has joined a group, they do not leave
- People will always join the best group they can
We need a method to determine which group is "best," a group fitness function. So, lets consider how the fitness of a group changes as people join the group. Every person the joins benefits the group in some way, but, if the group is large, adding another member will likely decrease the group's productivity. To simplify this a bit more, add the following assumptions:
- Every person contributes the same amount to the group.
- Every person hurts productivity by the same amount.
- Both of these amounts are quantifiable
Using these assumptions we can write the following equation:
\[ \frac{dF}{dn} = \alpha - \beta n \]
where:
- $ F $ is the fitness function.
- $ n $ is the number of people currently in the group
- $ α $ is an individual's contribution to the study group
- $ β $ is an individual's detriment to the study group
Let's explore this for a moment before moving on. Consider just $ \frac{dF}{dn} = α $. This piece of the equation tells us that as the number of people in the study group changes, the change in the fitness of the study group is proportional to $ α $, the individual contribution rate. But, we know that as the number of people increases, the effectiveness of the group decreases, so subtract something that grows as the population grows: $ β n $.
This equations is simple to solve, and we should impose the initial condition $ F(0) = 0 $, as a group with zero members has 0 fitness. The solutions then are:
\[ F(n) = \alpha n - \frac{\beta}{2} n^2 \]
Additionally, we probably want to know what the optimal study group size is. We can easily find (by setting $ \frac{dF}{dn} = 0 $) that the optimal size is $ \frac{\alpha}{\beta} $.
The Simulation
The simulation I have in mind is fairly simple.
- Someone shows up
- They evaluate all the study groups available to them
- They join the best on available (best evaluated using fitness function)
- If all available groups have even fitness, join one at random
- Repeat until there is no one left to join
Implementation and Results
I wrote some python code to see how this system would perform. I will leave the code at the bottom of the document. The results seem to correspond with reality.
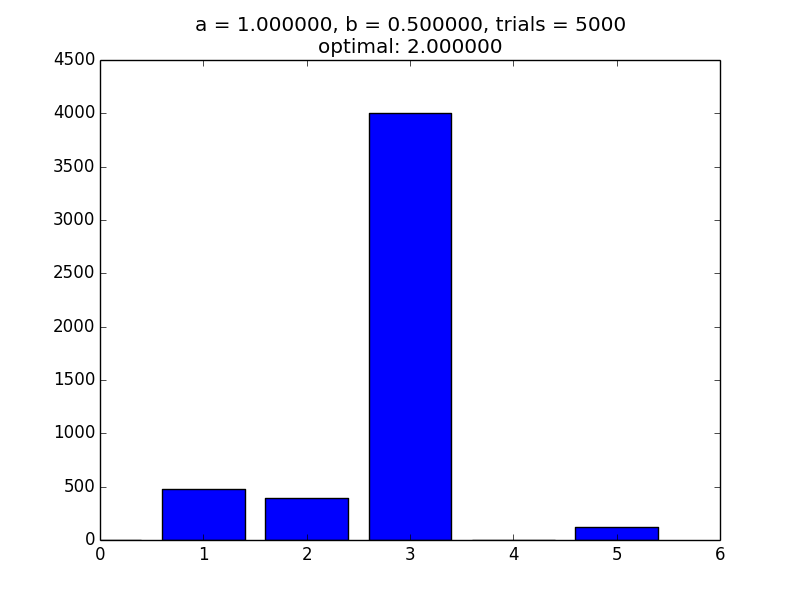
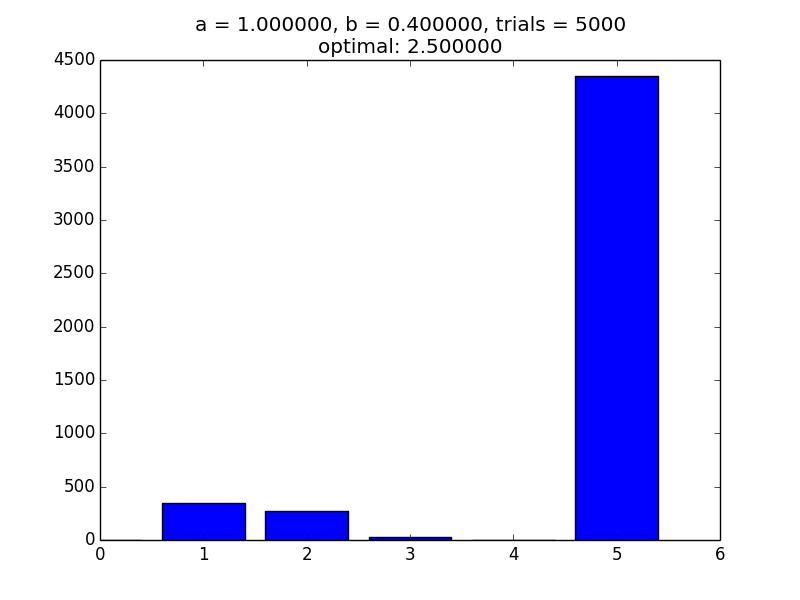
And here are links to all of the images I've generated at the time of writing.
Conclusion
From this model, it seems like we tend to form groups larger than would be optimal, because people continue to join the group once their joining will decrease the productivity of the group but would increase their personal productivity.
As I said at the top I do plan to explore this idea more. I hope to build a more complicated simulator allowing groups to split, experiment with a "selflessness factor," some chance that a person will not join a group if it hurts the group but helps the person, and a few other things. Please leave some feedback if this is interesting to you, we could discuss more ideas!
Simulation Code (not pythonic!)
from math import pow
from random import randint
###### Parameters
a = 1.0 # alpha define above
b = .5 # beta, also define above
maxgroups = 15
numjoiners = 10
###### Globals
pool = [0] * maxgroups
###### Functions
def fitness(n):
return a*n - (b/2)*pow(n,2)
##### Simulation
if __name__ == "__main__":
print("Starting the simulation")
for i in xrange(0, numjoiners):
best = (-1, None)
for index, fits in enumerate(map(fitness, pool)):
if best[1] == None or fits > best[1]:
best = (index, fits)
if best[0] > 0:
pool[best[0]] += 1
elif best[0] == 0:
pool[randint(0, len(pool) - 1)] += 1
else:
print("I refuse to join these groups")
break
print(pool)
print(map(fitness,pool))
print("optimal group size %d" % (a/b) )
print("average non_empty group size %d" %
(sum(pool) / len(filter(lambda a: a != 0, pool))))